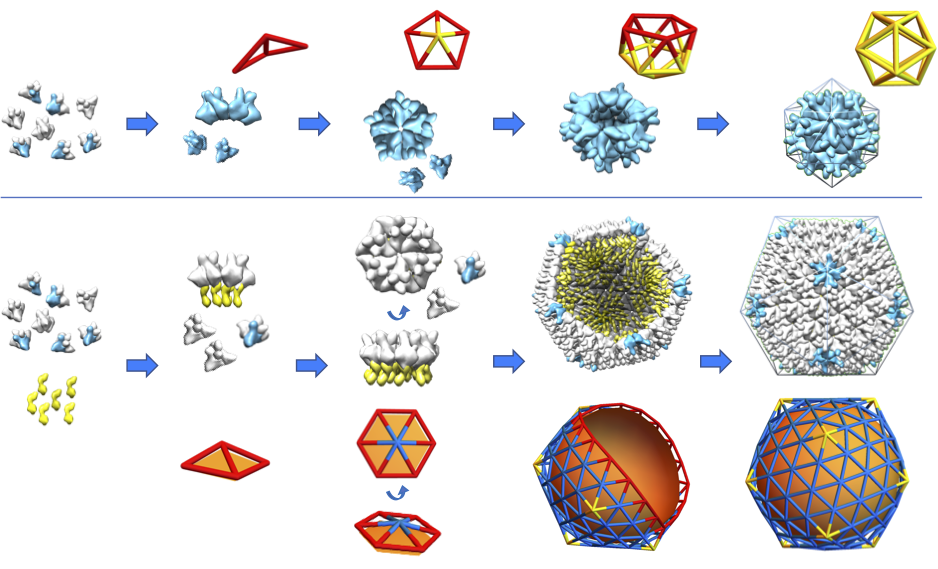
While small single-stranded viral shells encapsidate their genome spontaneously, many large viruses, such as the herpes simplex virus or infectious bursal disease virus (IBDV), typically require a template, consisting of either scaffolding proteins or an inner core. Using continuum elasticity theory, we study the growth of large viral shells (capsids) and show that a nonspecific template not only selects the radius of the capsid, but also leads to the error-free assembly of protein subunits into capsids with universal icosahedral order. We also performed a minimal model and simulate the assembly of a viral shell around a template under nonequilibrium conditions.

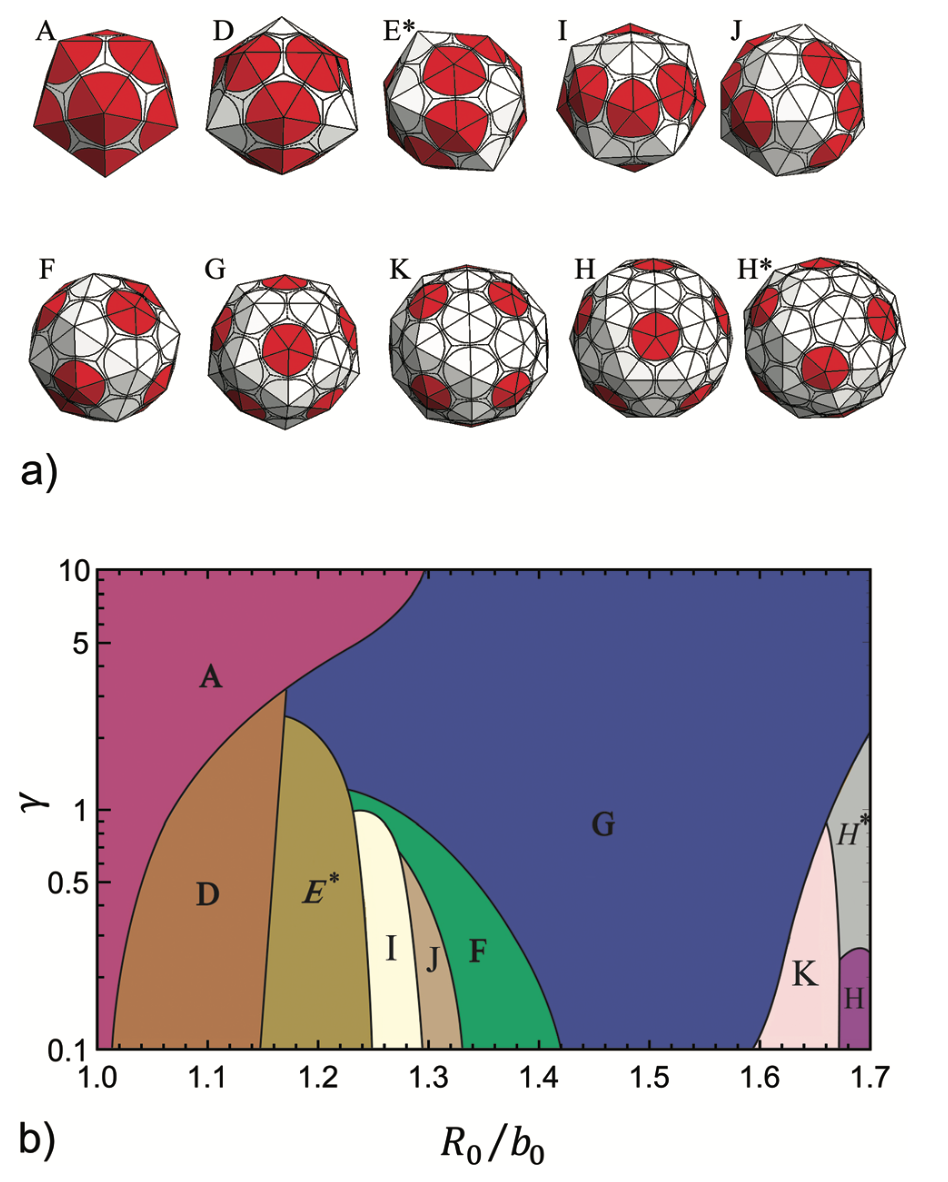
Understanding how highly symmetric, robust, monodisperse protein nano-cages self-assemble can have major applications in various areas of bio-nanotechnology, such as drug delivery, biomedical imaging and gene therapy. We develop a model to investigate the assembly of protein subunits into the structures with different sizes and symmetries. Using Monte Carlo simulation, we obtain global minimum energy structures. Our results suggest that the physical properties including the spontaneous curvature, flexibility and bending rigidity of coat proteins are sufficient to predict the size, symmetry and shape selectivity of the assembly products.

Many spherical viruses encapsulate their genomes in protein shells with icosahedral symmetry. This process is spontaneous and driven by electrostatic interactions between positive domains on the virus coat proteins and the negative genomes. We model the effect of the nonuniform icosahedral charge distribution from the protein shell instead using a mean-field theory. We find that this nonuniform charge distribution strongly affects the optimal genome length and that it can explain the experimentally observed phenomenon of overcharging of virus and viruslike particles.

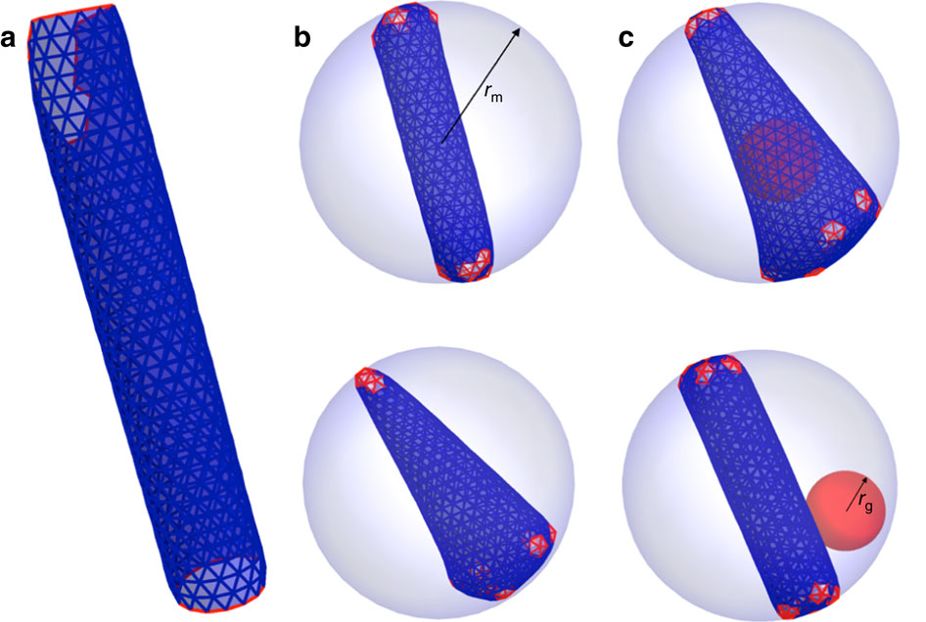
HIV-1 virions assemble as immature particles containing Gag polyproteins that are processed by the viral protease into individual components, resulting in the formation of mature infectious particles. There are two competing models for the process of forming the mature HIV-1 core: the disassembly and de novo reassembly model and the non-diffusional displacive model. We performed computer simulations and reveal the probable assembly pathways of HIV-1 capsid formation. Combining the experimental data and computer simulations, our results suggest a sequential combination of both displacive and disassembly /reassembly processes for HIV-1 maturation.

Helium is a universal wetting agent, in that it covers most materials with a thin layer. Garcia and Chan (PRL 83, 1187 (1999)), have discovered that helium films in the super-fluid phase are thinner than in the normal state. Until recently this difference in film thickness has remained unexplained. So-called Goldstone modes, associated with the broken symmetry of the superfluid state are known to be responsible for part, but not all, of the thinning.
We have shown that the flow field generated by surface fluctuations leads to a Casimir type force favoring thinner superfluid films. The combination of surface fluctuations and Goldstone modes is sufficient to account for the entirety of the thinning of the film in the Superfluid phase.

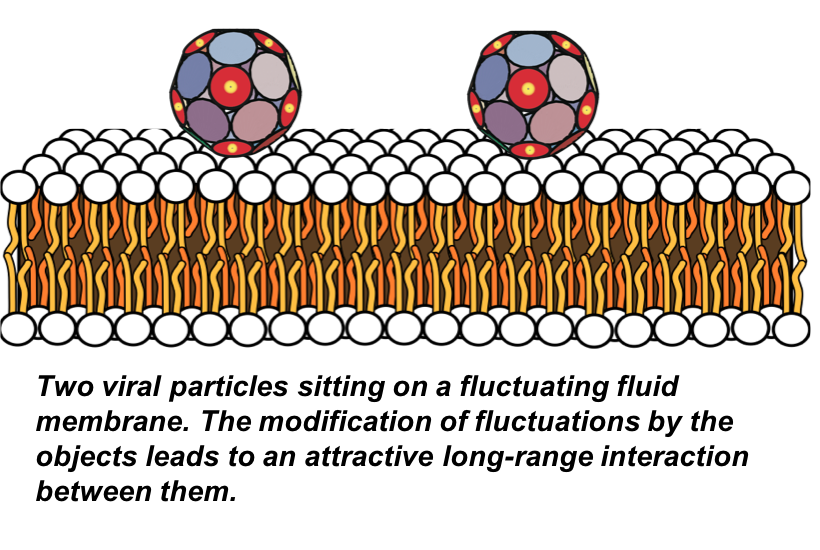
Biological membranes are formed by bilayers of amphiphilic lipid molecules with embedded macromolecules such as proteins. In general, the interactions between membrane inclusions depend on the separation between them and can be categorized as elastic and fluctuation-induced. The former is due to static elastic deformations induced in the membrane, while the latter is due to the modified entropy of the membrane fluctuations.
We have developed an exact method for calculating the fluctuation-induced forces between elastic inclusions of arbitrary shapes embedded in a fluctuating bio-membrane under tension, characterized by the surface tension and bending and Gaussian rigidities. The method allows to calculate the force in all ranges of parameters, all separations and all regimes inaccessible with previous theories.